Back to Mealy Machines
Example
1: NOT
Example 2: Vending Machine
Let's start with a simple Mealy machine that takes an input bit string b and produces the output NOT(b).
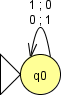
The machine should look like this, and can be downloaded through mealyNOT.jff:

A Mealy machine that produces NOT(b)
As you can see, the initial state has two outgoing transitions, one for the input "0" that produces the output "1", and one for the input "1" that produces the output "0". Thus, for every bit bi of the input, this machine produces the output NOT(bi), and takes the transition back to the same state so it may similarly process the next bit of the input.
Let's step the machine through the input "101".
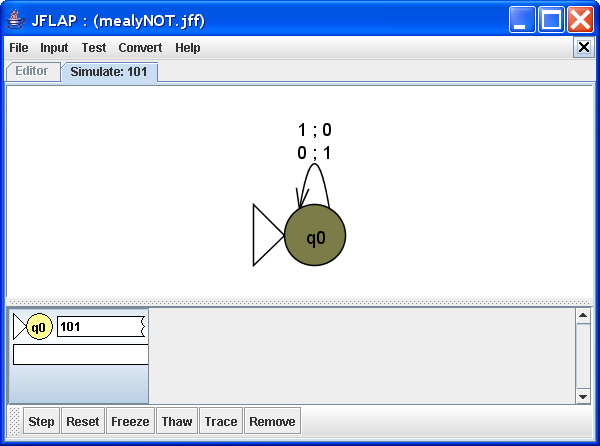
Initial set up
The machine is in its initial, and only, state, q0. The two outgoing transitions from q0 each produce the negation of the input bit. Click Step to process the next bit of the input.
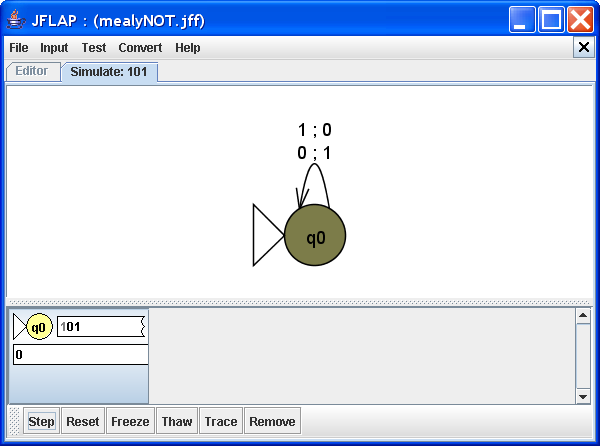
Step 1
Upon processing the first bit of the input, "1", the machine takes the transition 1 ; 0, producing the output "0", which is the negation of the input bit. This transition takes the machine back to its only state, q0. Click Step to process the next bit of input.
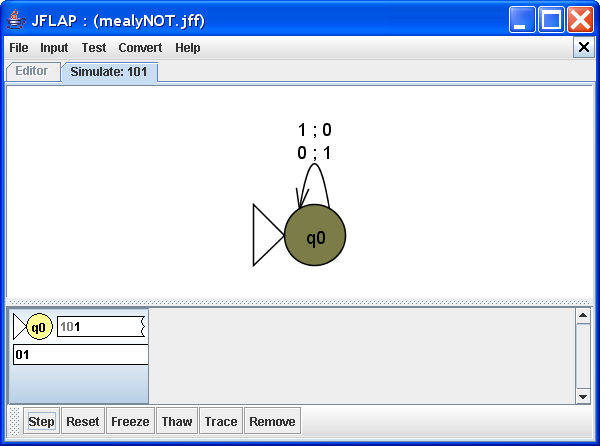
Step 2
Upon processing the next bit of the input, "0", the machine takes the transition 0 ; 1, producing the output "1", which is the negation of the input bit. This transition takes the machine back to q0. We have seen that state q0 properly processes both input bit "0" and "1", and returns the machine to q0, showing that the machine will properly process any input bit. Click Step to complete the process.
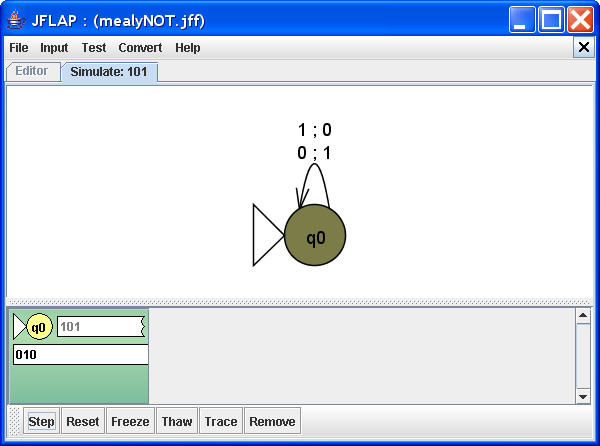
Step 3
As we can see, the machine indeed produces the negation of its input bit string.
We can also test this machine on multiple strings.
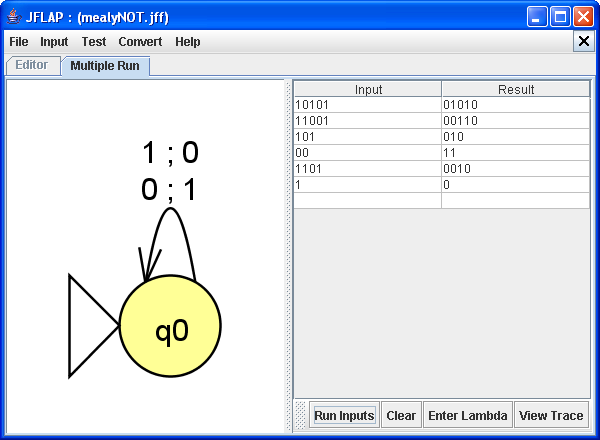
Testing the machine on multiple strings
As you can see, it produces NOT(b) in every instance.
You can download the file here to try it out.
(Example adapted from Theory of Finite Automata with an Introduction to Formal LanguagesK by John Carroll and Darrell Long.)
Next, let's consider a more complex machine. We shall build a vending machine that dispenses one piece of candy once enough money has been inserted, and returns the appropriate amount of change. (To see a completed version, feel free to download mealyVending.jff.)
Let V = ({0c, 5c, 10c, 15c}, {n, d, q}, {c0, c1, c2, c3, c4}, δ, ω, 0c}. (See the Mealy machine definition.) V describes a vending machine that dispenses 20¢ candy bars.
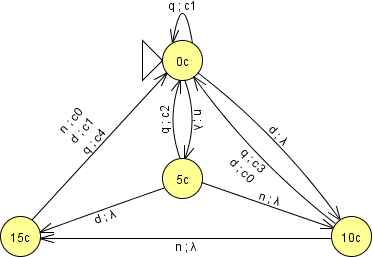
Mealy machine V
This Mealy machine has four states, 0c, 5c, 10c, and 15c, each describing the amount of money inserted in the vending machine, 0¢, 5¢, 10¢, and 15¢. Its input alphabet of n, d, and q, denotes the insertion of nickels, dimes, and quarters respectively. In its output alphabet, λ denotes the vending machine doing nothing, while c0, c1, c2, c3, and c4, denote the machine dispensing candy and no, one, two, three and four nickels respectively as change.
Let's step through the input ndq. (That is, someone inserted a nickel, a dime, followed by a quarter.)
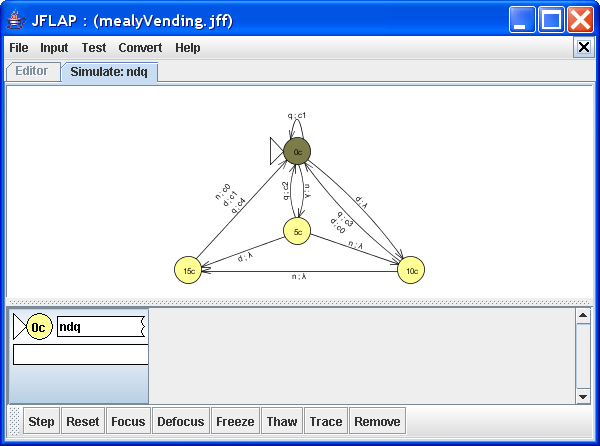
No coins inserted
The machine starts at 0c, as it has not had any money inserted yet. Click Step to insert the first nickel.
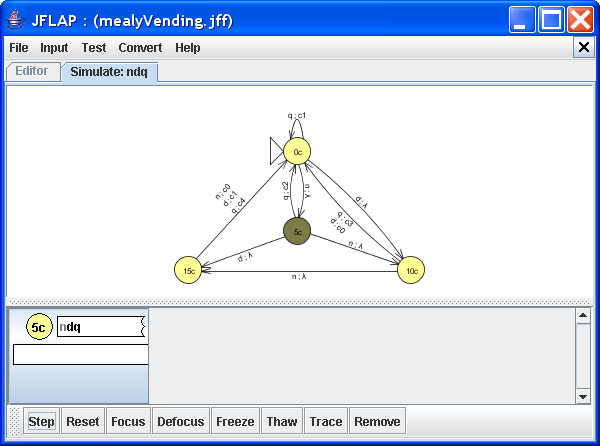
First coin (a nickel) inserted
The machine takes the transition n ; λ from 0c to 5c, denoting that 5¢ has been inserted. The transition produces no output as not enough money has been inserted. Click Step to insert the next coin, a dime.
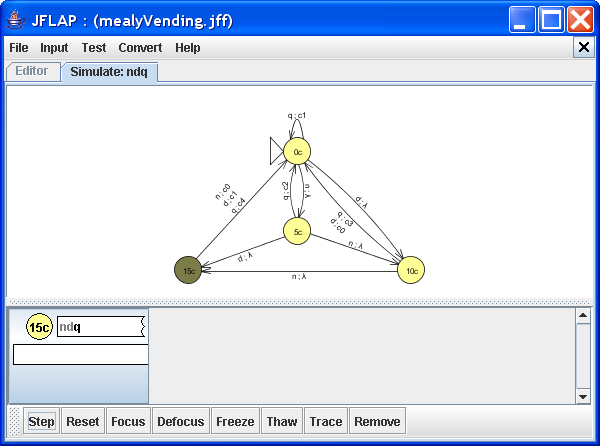
Second coin (a dime) inserted
The machine takes the transition d ; λ from 5c to 15c, indicating that 15¢ has been accumulated. Again, the transition produces no output as not enough money has been inserted. Click Step to insert the last coin, a quarter.
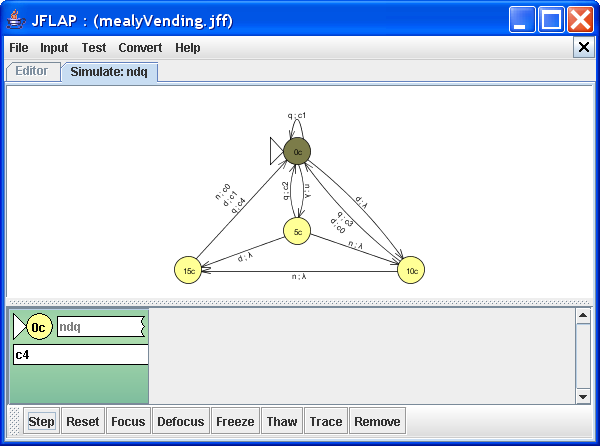
Last coin (a quarter) inserted
The machine takes the transition q ; c4 from 15c to 0c, back to the initial state. The transition produces output c4, and the vending machine dispenses a piece of candy and four nickels. Thus, once it has accumulated sufficient money, it dispenses a piece of candy and the correct amount of change, just as we have described.
Let's try our vending machine out on different sets of change.
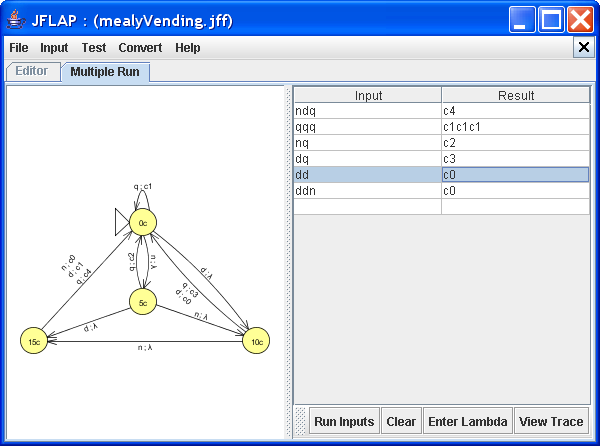
Running the vending machine on different sets of coins
As you can see, each time our vending machine accumulates sufficient money, it dispenses a piece of candy and the appropriate amount of change. The last two inputs, dd and ddn, although different, produce the same output c0. This is because they end in different states. Effectively, for input ddn the vending machine still has 5¢ in it.
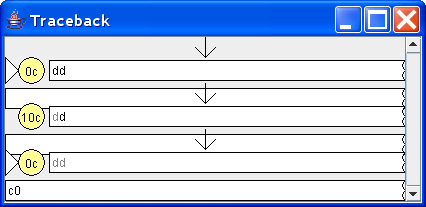
The trace for input dd
For input dd, the state we end in is 0c, indicating there is no extra change in the vending machine.
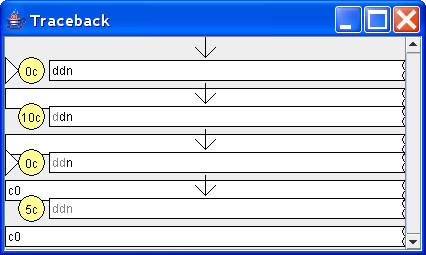
The trace for input ddn
For input ddn, the state we end in is 5c, indicating that we still have 5¢ of change in it.