Definition
Differences
between a Mealy Machine and an FA
Proceed to Mealy Machine Examples
JFLAP defines a Mealy machine M as the sextuple M = (Q, Σ, Γ, δ, ω, qs) where
Q is a finite set of states {qi | i
is a nonnegative integer}
Σ is the finite
input alphabet
Γ is the finite output
alphabet
δ is the transition function, δ
: Q × Σ →
Q
ω denotes the output function, ω
: Q × Σ →
Γ
qs (is a member of
Q) is the initial state
Mealy machines are different than Moore machines in the output function, ω. In a Mealy machine, output is produced by its transitions, while in a Moore machine, output is produced by its states.
To start a new Mealy machine, select the Mealy Machine option from the main menu.
Starting a new Mealy machine
A Mealy machine is very similar to a Finite Automaton (FA), with a few key differences:
It has no final states.
It does not accept or reject input, instead, it generates output from input.
Lastly, Mealy machines cannot have nondeterministic states.
Let's go through these points.
In an FA, when you have the Attribute Editor tool selected (you
may do so by clicking the
button), right-clicking on a state it will produce a pop-up menu that
allows you to, among other things, set it to be a final state. In a
Mealy machine, that option is not available.
|
|
|
|
An FA state menu |
A Mealy machine state menu |
A Mealy machine does not have final states because it does not accept or reject input. Instead, each transition produces output, which will be described below.
A Mealy machine produces output each time it takes a transition.
Creating a Mealy machine is the same as creating an FA with the exception of creating its transitions. In a Mealy machine, each transition produces output. When you are creating a transition, two blanks appear instead of one. The first blank is for the input symbol, the second blank is for the output symbol.
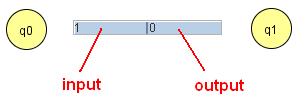
Creating a transition
When the transition is created, its label will be two symbols separated by a semicolon, ";". The input symbol is to the left of the semicolon, and the output symbol is to its right.
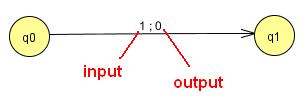
Transtion created
Thus, when in q0 with input of "1", the machine will take the transition to q1 and produce the output "0".
With each transition producing output, the Mealy machine can produce output from an input string.
Instead of accepting or rejecting input, a Mealy machine produces output from an input string.
Let's look at this simple Mealy machine, which can be downloaded through mealyNOT.jff:
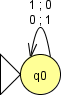
A simple Mealy machine
When we select the menu option Input : Step... and enter your input, we get a display similar to that of an FA, except with another piece of tape below the input tape. This displays the output of the machine at the current step.
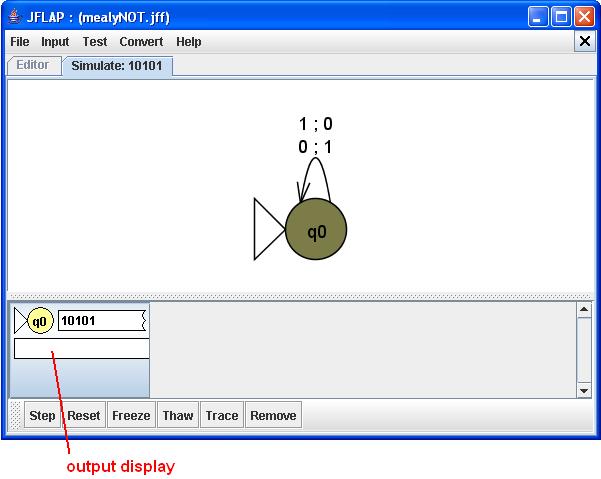
The output display
At each step. The output tape updates itself to display the total output that has been produced so far:
|
Initial: |
Step 1: |
Step 2: |
. . . |
Final: |
|
|
|
|
. . . |
|
The menu option Input : Fast Run... works similarly, with the output being displayed in a tape under the input tape:
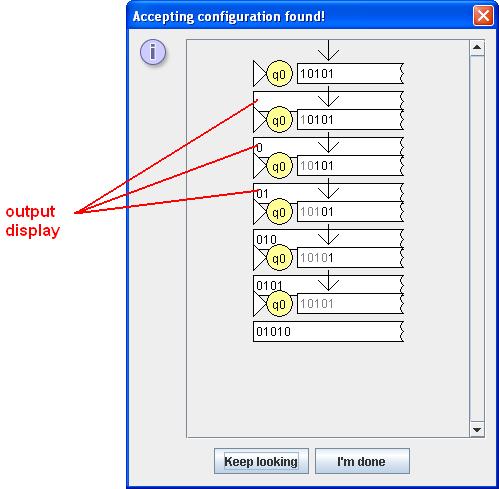
Fast run output display
Similarly, when we select Input : Multiple Run, output is displayed in the Result column.
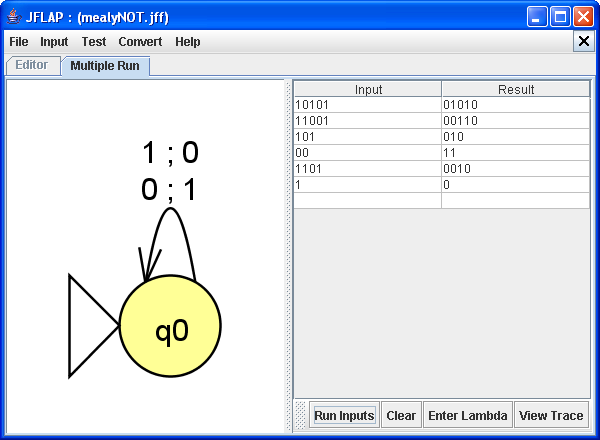
Multiple run output display
As Mealy machines map an input to a unique output, nondeterminism cannot exist in a Mealy machine. Although we still will be able to build a Mealy machine that has nondeterminism, we will not be able to run input on it.
For instance, let's modify our machine slightly to make:
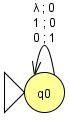
Mealy machine with nondeterminism
We we try to run it on an input, with Input : Step..., Input : Fast Run..., or Input : Multiple Run..., we will get an error message asking us to remove the nondeterministic states:
Select Test : Highlight Nondeterminism to view the nondterministic states. Remove the nondeterminism in order to be able to run input on the Mealy machine.
This concludes our brief tutorial on Mealy machines. Thanks for listening!
View Mealy machine examples.
View
Moore machines.
